Yaritza Soto
C.I:22.398.789
ING. Industrial
Elemento de Maquina
Resortes Helicoidales

Resortes Helicoidales

Los resortes o muelles helicoidales son elementos mecánicos que se montan entre dos partes mecánicas de una máquina, con el fin de amortiguar impactos o de almacenar energía y devolverla cuando sea requerida. Consiste en un arrollamiento de espiras de alambre normalmente redondo y de sección cuadrada o rectangular; el material del alambre debe poseer alto límite de elasticidad para que cumpla con las solicitaciones indicadas.

Tipos de resortes:
De acuerdo a las fuerzas o tensiones que puedan soportar, se distinguen tres tipos principales de resortes:

• Resortes de tracción: Estos resortes soportan exclusivamente fuerzas de tracción y se caracterizan por tener un gancho en cada uno de sus extremos, de diferentes estilos: inglés, alemán, catalán, giratorio, abierto, cerrado o de dobles espira. Estos ganchos permiten montar los resortes de tracción en todas las posiciones imaginables.

Resorte cónico de compresión.

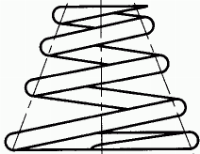
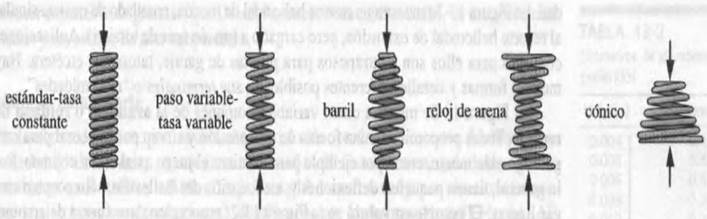
• Resortes de compresión: Estos resortes están especialmente diseñados para soportar fuerzas de compresión. Pueden ser cilíndricos, cónicos, icónicos, de paso fijo o cambiante.

• Resortes de torsión: Son los resortes sometidos a fuerzas de torsión (momentos).

Existen resortes que pueden operar tanto a tracción como a compresión. También existen una gran cantidad de resortes que no tienen la forma de resorte habitual; quizás la forma más conocida sea la arandela grower.




Materiales de un Resorte Helicoidal :


Los muelles mecánicos sirven para ejercer esfuerzos, proporcionar flexibilidad, almacenar o absorber energía.  Pueden dividirse en muelles de alambre o de lámina, los muelles de alambre comprenden los resortes helicoidales y alambre redondo o cuadrado y sirven para resistir esfuerzos de tracción, compresión o torsión.  Los muelles de láminas pueden ser de tipo elíptico o de voladizo.






Ejercicio de un Resorte Helicoidal:


Problema n° 1) Un cuerpo de 4 kg. de masa está sujeto aun resorte helicoidal, y oscila verticalmente con movimiento armónico simple. La amplitud es de 0,5 m, y en el punto más alto del movimiento el resorte tiene su longitud natural. Calcúlese la energía potencial elástica del resorte, la energía cinética del cuerpo, su energía gravitacional respecto al punto más bajo del movimiento y la suma de estas tres energías, cuando el cuerpo está:
a) En su punto más bajo.
b) En su posición de equilibrio, y
Cuando está en su punto de equilibrio la energía E_p = 0, porque X = 0.
c) En su punto más alto.

Desarrollo

m = 4 kg
A = 0,5m
k = F/x
k = m.g/x
4.9,8/0,5 = 78,4 N/m

a)
E_p = k.x²/2
E_c = m.v²/2 = 0
E_p = 78,4.5²/2
9,8 J
Ec = 0 porque su velocidad es cero.
E _pg = m.g.h/2 = 0 porque la h (altura es 0).
E_T = E_p + E_c + E _pg = 9,8N.m
b)

entonces:
Ec = 4.2,21²/2
9,76 J
E _pg = m.g.h/2 = 4.9,8.0,5/2 = 9,8 J
E_T = E_p + E_c + E _pg = 19,56 J
c)
E_p = k.x²/2
E_c = m.v²/2 = 0
Como es en este caso para el punto mas alto se considera la energía como negativa, definida así por su amplitud (-A).
E_p = 78,4.0,5²/2 = -9,8 J
E _pg = m.g.h/2 = 4.9,8.1/2 = 19,6 J
E_T = E_p + E_c + E _pg = 9,8 N.m


Ejercicio de Resorte :


Problema n° 2) Una masa de 100 kg. Suspendida de una alambre cuya longitud natural to es de 4m, lo alarga 0,004m. La sección transversal del alambre, que se puede suponer constante, es 0,1 cm².
a) Si se desplaza la carga hacia abajo una pequeña distancia y se abandona a sí misma, determínese a que frecuencia vibrará.
b) Calcúlense el módulo de Young del alambre.

Desarrollo

m = 100 kg
l₀ = 4 m
Δl = 0,004 m
A = 0,1 cm²
a)
k = m.g/l
k = 100 kg.(9,8 m/s²)/0,004 m
k = 245000 kg.s^-2
f = (1/2.π).√k/m
f = (1/2.π).√245000/100
f = 7,87 Hz
b)
Y = F.l₀ /A.Δl
F = k.x
F = 245000.0,004
F = 980 kg.m.s^-2
Y = 980*4/0,004.10^-5
Y = 98.10¹⁰